Exercices corrigés : Construction de parallélogrammes

Fiche d'exercices N°1 - correction fiche d'exercices N°1. Fiche d'exercices N°2 - correction fiche d'exercices N°2. Fiche d'exercices N°3 - correction fiche d'exercices N°3. Fiche d'exercices N°4 - correction fiche d'exercices N°4. Fiche d'exercices N°5 - correction fiche d'exercices N°5. Fiche d'exercices N°6 - correction fiche d'exercices N°6. Fiche d'exercices N°7 - correction fiche d'exercices N°7. Fiche d'exercices N°8 - correction fiche d'exercices N°8. Fiche d'exercices N°9 - correction fiche d'exercices N°9. Fiche d'exercices N°10 - correction fiche d'exercices N°10.

Résumé de cours : Construction de parallélogrammes

Introduction

Imaginez un monde où les côtés opposés sont toujours parallèles et où les angles opposés sont toujours égaux. Bienvenue dans le monde des parallélogrammes! Ensemble, découvrons leurs secrets.

Prérequis

Avant de plonger dans cet univers, assurez-vous de connaître les bases des angles, des droites parallèles et des quadrilatères. Si vous êtes prêt, allons-y!

Objectif et Attentes

À la fin de cette aventure, vous serez non seulement capable d'identifier les différents types de parallélogrammes, mais aussi de les dessiner avec précision et de comprendre pourquoi ils sont si spéciaux.

Compétences Développées

• Reconnaître et différencier les types de parallélogrammes.
• Dessiner des parallélogrammes avec confiance.
• Comprendre et expliquer les propriétés uniques des parallélogrammes.

Un Petit Rappel

Un parallélogramme est un quadrilatère (une figure à quatre côtés) dont les côtés opposés sont toujours parallèles. Cela signifie qu'ils ne se rencontrent jamais, peu importe combien vous les prolongez!

Types de Parallélogrammes et Leurs Propriétés

Il existe différents types de parallélogrammes, et chacun a ses propres caractéristiques spéciales. Jetons un oil à chacun d'eux :

• Parallélogramme simple : Les côtés opposés sont parallèles et égaux. Les angles opposés sont égaux. C'est la forme la plus générale.
• Rectangle : C'est un parallélogramme, mais avec un petit plus : tous ses angles sont droits!
• Losange : Tous ses côtés sont de même longueur. C'est comme un "carré incliné".
• Carré : C'est le roi des parallélogrammes! Il a tous les côtés de même longueur et tous les angles droits.

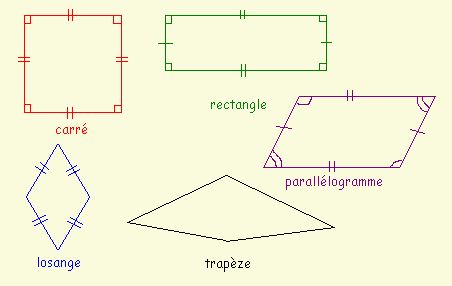
Conseil pédagogique : Imaginez un carré. Si vous le "poussez" d'un côté, il devient un losange. Si vous le "tirez" d'un coin, il devient un rectangle. Si vous le "poussez" et le "tirez" en même temps, il redevient un parallélogramme simple!

Exemples et Exercices

Exemple 1

Comment pouvez-vous être sûr qu'une figure est un rectangle et non un autre type de parallélogramme?

Réponse : Vérifiez les angles! Si tous les angles sont droits, c'est un rectangle.

Exercice 1

Vous avez une figure avec tous les côtés de même longueur, mais seulement deux angles droits. Quelle est cette figure?

Correction

C'est un losange! Rappelez-vous, un losange a des côtés égaux, mais pas nécessairement des angles droits.

Applications Pratiques

Les parallélogrammes sont partout! Des terrains de jeux aux motifs de carrelage, en passant par les designs architecturaux. La prochaine fois que vous verrez une figure à quatre côtés, demandez-vous : est-ce un parallélogramme?

Résumé

Les parallélogrammes sont des quadrilatères spéciaux avec des côtés opposés parallèles. Il existe différents types, chacun avec ses propres caractéristiques. Avec ces connaissances, vous pouvez maintenant identifier et dessiner différents parallélogrammes avec confiance!

Conseils et Erreurs à Éviter

• Ne présumez pas qu'un quadrilatère est un parallélogramme sans vérifier les côtés et les angles.
• Utilisez toujours une équerre pour vérifier les angles droits.
• Pratiquez le dessin de différentes formes pour mieux les comprendre.