Décomposer les Nombres Décimaux - Exercices PDF à Télécharger avec Corrigés

Ces fiches d’activités sont conçues pour aider les élèves de 6^e à maîtriser la décomposition des nombres décimaux. À travers des exercices progressifs, les élèves apprennent à exprimer un nombre sous différentes formes : développement décimal, fractionnaire ou positionnelle. Une compétence fondamentale pour la compréhension du système décimal.

Les documents sont prêts à être imprimés et accompagnés de leurs corrigés détaillés. Parfait pour s’exercer en autonomie ou comme support pédagogique en classe.

Fiches à télécharger - Nombres décimaux (décomposition)

Fiche d'exercices N°1 - correction fiche d'exercices N°1. Fiche d'exercices N°2 - correction fiche d'exercices N°2. Fiche d'exercices N°3 - correction fiche d'exercices N°3. Fiche d'exercices N°4 - correction fiche d'exercices N°4. Fiche d'exercices N°5 - correction fiche d'exercices N°5. Fiche d'exercices N°6 - correction fiche d'exercices N°6. Fiche d'exercices N°7 - correction fiche d'exercices N°7. Fiche d'exercices N°8 - correction fiche d'exercices N°8.

Résumé de cours : Décomposition des nombres décimaux

Définition des nombres décimaux

Un nombre décimal est un nombre qui possède une partie entière et une partie décimale, séparées par une virgule. Par exemple :

• 15,47
• 3 217,019
• 0,0037

Décomposition en milliers, centaines, dizaines, unités, dixièmes, centièmes, millièmes

Pour décomposer un nombre décimal en ses différentes composantes, on suit ces règles :

• À gauche de la virgule : unités, dizaines, centaines, milliers
• À droite de la virgule : dixièmes, centièmes, millièmes

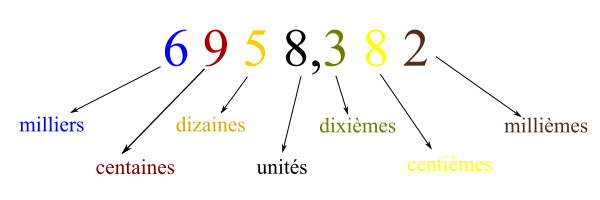
Exemples de décomposition :

• 15,47 = 1 × 10 + 5 × 1 + 4 × 1/10 + 7 × 1/100
• 3 217,019 = 3 × 1000 + 2 × 100 + 1 × 10 + 7 × 1 + 0 × 1/10 + 1 × 1/100 + 9 × 1/1000
• 0,037 = 0 + 3 × 1/100 + 7 × 1/1000
• 3 215,625 = 3 × 1000 + 2 × 100 + 1 × 10 + 5 × 1 + 6 × 1/10 + 2 × 1/100 + 5 × 1/1000

Exemples

10 exemples pour s'entraîner à la décomposition :

• 235,04 = 2 × 100 + 3 × 10 + 5 × 1 + 4 × 1/100
• 9,126 = 9 × 1 + 1 × 1/10 + 2 × 1/100 + 6 × 1/1000
• 17,909 = 1 × 10 + 7 × 1 + 9 × 1/10 + 9 × 1/1000
• 5 432,321 = 5 × 1000 + 4 × 100 + 3 × 10 + 2 × 1 + 3 × 1/10 + 2 × 1/100 + 1 × 1/1000
• 0,015 = 0 + 1 × 1/100 + 5 × 1/1000
• 678,055 = 6 × 100 + 7 × 10 + 8 × 1 + 5 × 1/100 + 5 × 1/1000
• 0,87 = 8 × 1/10 + 7 × 1/100
• 1 232,123 = 1 × 1000 + 2 × 100 + 3 × 10 + 2 × 1 + 1 × 1/10 + 2 × 1/100 + 3 × 1/1000
• 8,21 = 8 × 1 + 2 × 1/10 + 1 × 1/100
• 4,009 = 4 × 1 + 9 × 1/1000

Autres points à connaître

• La décomposition aide pour l’addition, la soustraction, la multiplication et la division des nombres décimaux.
• En addition ou en soustraction, il faut bien aligner les chiffres selon leur rang (unités, dixièmes, etc.).
• Lorsqu’on multiplie ou divise, il peut être utile de déplacer la virgule pour faciliter le calcul.
• Les nombres décimaux peuvent être comparés avec les symboles >, < et =.
• Comprendre la position de la virgule est essentiel pour décomposer correctement un nombre.